I intend to build up this guide into a series of more complex “lessons” so eventually we can read packets as they are on the wire and you will be able to interpret what you are seeing without too much difficulty.
Time to start with the basics. In order to understand and read packets, we need to know the fundamentals. How do computers and network communicate? Essentially by binary and hexadecimal. This is a series of zero’s and one’s and the numbers 0 to 9 with the letters A to F.
When I was taught this in school, some 20ish years ago, I honestly found it a bit complicated, but looking back it was only complicated due to the way it was taught. Hopefully this methodolgy is simple for you to understand.
Counting in binary is not too difficult, the values can only be a 0 or a 1, an off or on value. However what the off or on values represent is the important ‘bit’.
You essentially have 8 bits in a byte and this makes binary reasonably straight forward, for counting I find it best to create a quick table, this allows me to visually count, rarther than attempting to work out everything in my head.
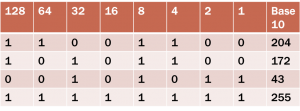 What the chart shows, we have the 8 bits represented across the top. The numbers 128 down to 1. The base 10 is the representation of the value in decimal, the numbers we are familar with. The values 128 to 1 are powers of 2.
What the chart shows, we have the 8 bits represented across the top. The numbers 128 down to 1. The base 10 is the representation of the value in decimal, the numbers we are familar with. The values 128 to 1 are powers of 2.
We have the following
20 = 1
21 = 2
22 =4
23 =8
24 = 16
This is essentially doubling up each time, and this is how binary works and is pretty straight forward.
In my example above, we have a a value of 1 in the columns that represent 128, 64, 8 and 4. So all we do now is add these up.
128+64+8+4 = 204
128+32+4+4 = 172
32+8+2+1=43
128+64+32+16+8+4+2+1=255
For me this chart makes it easy, whenever I am required to convert binary into decimal, I always create the chart on a bit of scrap, fill in the relevant fields and add them up.
Now you can work out Hexadecimal in a similar way, which I find is far easier for my poor brain to understand. When I was taught hex in school, I was taught to convert the hex to binary and then into decimal, which you can do, however it creates an extra step, which takes longer and there is one extra step to make a mistake.
Hexadecimal
Base16
0 to F
Seems complicated? Not really, its as easy as binary.
160 = 1 = 20
161 = 16 = 24
162 = 256 = 28
163 = 4096 = 212
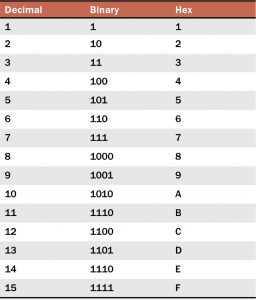
This simple hex chart covers what you need to know. Starts from 0 to 9, decimal 10 to 15 is represented with A to F.
So how do we calculate hex values? I will show you the same methodolgy that I use for binary conversion. A nice and simple chart.
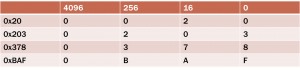 So what does this mean exactly? Well we do a similar method to binary.
So what does this mean exactly? Well we do a similar method to binary.
We have 0x20 which is how we represent hex, when you see it in this format, it us telling you this is a hexadecimal value.
0x20 = (2 x 16) + (0 x 1) = 32 + 0 = 32 decimal
0x203 = (2 x 256) + (0 x 16) + (3 x 1) = 512 + 0 + 3 = 515 decimal
0x378 = (3 x 256) + (7 x 16) + (8 x 1) = 768 + 112 + 8 = 888 decimal
0xBAF = (11 x 256) + (10 x 16) + (15 x 1) = 2816 + 160 + 15 = 2991 decimal
So in the first example, we have the hex value of 20. So these fill in the 2 colums on the right, 2 in the 16 value and 0 in the 1 value. To calculate we just multiple 2 by 16, so we have 32. 0 multiplied by 1 is 0, so the total value in decimal is 32.
The second example, we have 0x203, so using the same formula we have to multiply 2 by 256, multiply 0 by 16 and multiply 3 by 1, and we then just add these figures up giving us the total of 515 decimal.
Simples.
Like it!
You should slap it so anyone can comment not just registered users, otherwise there’ll be not many comments.
Chat soon, bro =D
Yeah I need to find something to stop the spam, I dont want all those bots to just fill comments with drug spam.
How are things with you? We need to catch up sometime!
Good! Busy! PhD’s a massive time vampire – but I did finally write a software library as one of my papers:
https://github.com/FedUni/caliko
Took me like 18 months to get that thing working properly… just crazy.
Looks like things are going well for you – which is fantastic. Ping me an email some and we can chat =D